La compression d’images
1 Introduction
On essayera dans ce document de présenter les principes fondamentaux et quelques exemples de compression dans le domaine des images.
2 Principe
Le principe des compressions est simple. Comprimer c’est diminuer la place que prennent des données en supprimant les informations redondantes et/ou inutile. Les images naturelles en étant riches, il devient tout naturel qu’elles soient un des sujets de prédilections des compressions.
Dans la compression, on distingue deux grandes familles très différentes. Il y a les compressions non destructrices dites entropiques et les autres dites destructrices. Les compressions entropiques sont souvent facilement généralisables à tous les types de données. Il n’en est pas de même pour les compressions destructrices qu’il faut adapter aux données afin de ne perdre que les informations de moindres importances. Les images permettent bien ce genre de compression grâce à des particularités qui leur sont propres.
3 Particularités
3.1 Le codage Luminance, Chrominance
Il est reconnu depuis longtemps que notre œil est plus sensible à la luminance (l’intensité de la lumière) qu’à la chrominance (les couleurs). La première technique pour réduire la taille d’une image est donc de donner plus d’importance aux informations de luminance que de chrominance qui seront codées sur un espace moins important. D’ailleurs, c’est ce qui est utilisé depuis longtemps dans les systèmes de diffusion de télévision Hertzienne.
Si on part du codage d’un pixel en Rouge, Vert et Bleu, on obtient 3 variables Y (luminance), Cr (chrominance) et Cb (chrominance aussi) données par les formules qui suivent :
| Y | = 0,299 * Rouge + 0,587 * Vert + 0,114 * Bleu | |
| Cr | = Rouge – Y | |
| Cb | = Bleu – Y | |
(l’œil est beaucoup plus sensible au vert)
Le retour au Rouge, Vert et Bleu est données par :
| Rouge | = Cr + Y |
| Bleu | = Cb + Y |
| Vert | = Y * 1,7 – Rouge* 0,509 – Bleu * 0,194 |
La compression tient dans le fait que l’on supprime carrément des informations de chrominance. Prenons l’exemple du codage dit 4:1:1.
 |
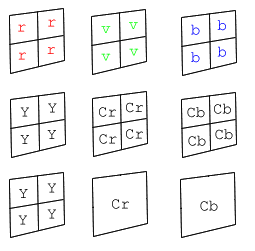Couleur composées de Rouge, Vert et Bleu
Décomposition Y Cr Cb Suppression de Cr et Cb (moyenne des 4) |
Ce principe-là est présent dans la compression JPEG.
Voici une implémentation en C (entièrement libre de droits) des fonctions de conversion entre le mode YUV et le mode RGB. Les calculs sont un peu compliqués car ils sont fait sur des entiers.
/* définie un pixel en Rouge, Vert, Bleu (comme pour un écran) */
typedef struct RGB
{
unsigned char r,g,b;
} RGB;
/* définie un pixel en Luminance Chrominance (utilisé pour stocker */
/* l'image par exemple) */
typedef struct YUV {
unsigned char Y;
char Cr,Cb;
} YUV;
/* fonction de convertion de RGB vers YUV */
YUV RGB2YUV(RGB colRGB)
{ YUV local;
unsigned short localY;
short localCb,localCr;
/* Y = 0,299*R + 0,587*G + 0,114*B (G comme Green = Vert) */
localY = ( 76*(unsigned short)colRGB.r)
+(150*(unsigned short)colRGB.g)
+( 30*(unsigned short)colRGB.b);
local.Y = (unsigned char)(localY>>8);
localCr = colRGB.r - local.Y; /* Cr = R - Y */
local.Cr = localCr>>1;
localCb = colRGB.b - local.Y; /* Cb = B - Y */
local.Cb = localCb>>1; /* on divise par 2 pour ne pas avoir */
return (local); /* de debordement */
}
/* fonction de convertion de YUV vers RGB */
RGB YUV2RGB(YUV colYUV)
{ RGB local;
long localg;
short localr,localb;
/* on remultiplie par 2 (<<1)*/
localr = (colYUV.Cr<<1) + colYUV.Y; /* R = Cr + Y */
if(localr<0) local.r = 0; else
if(localr>255) local.r = 255; else /* si cela deborde, on sature */
local.r = (unsigned char)localr;
localb = (colYUV.Cb<<1) + colYUV.Y; /* B = Cb + Y */
if(localb<0) local.b = 0; else
if(localb>255) local.b = 255; else /* si cela deborde, on sature */
local.b = (unsigned char)localb;
/* G = Y*1,7 - R*0,509 -B*0,194*/
localg = ( (long)(colYUV.Y)*256 - (long)(localr)*76 - (long)(localb)*30)/150;
if(localg<0) local.g = 0;
else if(localg>255) local.g = 255;
else local.g = localg;
return (local);
}
4 Compression non destructrice
Ces compressions sont applicables à tous les types de données mais les taux de compression reste la plupart du temps faibles.
4.1 L’entropie
L’entropie indique le nombre de bits minimum qu’il faut par pixel pour stocker notre image (longueur moyenne minimale en bits d’un pixel).
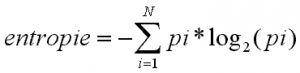
N étant le nombre de valeur prise par nos données et pi la probabilité d’avoir la valeur i. Grâce à cela, on peut vite évaluer une compression.
4.2 RLE (codage de taille)
C’est l’un des principes les plus simples. Au lieu de coder plusieurs fois une valeur lorsqu’elle apparaît plusieurs fois à la suite, on code le nombre de fois ou elle est présente. Ceci est applicable de bien des manières.
Exemple :
| la chaîne (en hexa) | : 0F F2 F2 F2 F2 84 32 32 32 |
| peut donner | : 0F 01 F2 04 84 01 32 03 |
Attention cela peut aussi parfois augmenter la taille.
4.3 HUFFMAN (code à taille variable)
C’est un principe très intéressant et assez performant. Il s’agit non plus de coder nos données sur un nombre fixe de bits mais de coder les valeurs qui reviennent souvent sur peu de bits et au contraire sur beaucoup plus les valeurs rares.
Exemples :
| Probabilité | Valeur (binaire) | Code par Huffman |
Toute la difficulté réside dans la recherche du codage. On utilise ce qui est appelé l’arbre de Huffman.
Voici l’arbre que cela donnerait pour notre exemple :
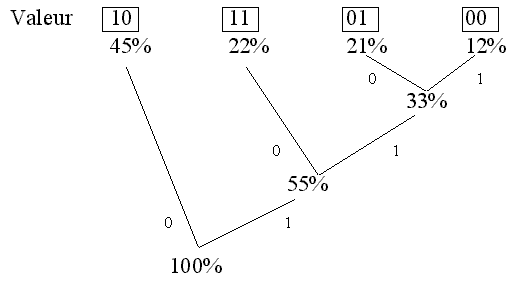
L’arbre est construit en mariant toujours les deux pourcentages les plus faibles.
5 Compression destructrice
Ici, on rentre dans le domaine des compressions avec perte d’information. Le but est de perdre le minimum d’information de manière à garder un aspect visuel le plus proche. Ces compressions ne sont pas adaptables à toutes les données mais l’on retrouve les mêmes concepts dans la compression du son. Ces compressions se font souvent en deux étapes. Dans la première étape, on transforme nos pixels (par exemple nos données luminance Y) dans un nouvel espace de manière à concentrer les informations importantes sur un nombre plus faible de données. L’étape de quantification consiste à approximer (moins de bits) les nouvelles données les moins importantes voire carrément les supprimer.
5.1 Etape de transformation
5.1.1 DCT (Discrete Cosine Transform)
La DCT est basée sur le même principe que la transformée de Fourrier. On recherche dans notre image l’importance de fonctions de base qui toute additionnées donnent nos données.
Exemple de DCT dans un repère 1D :
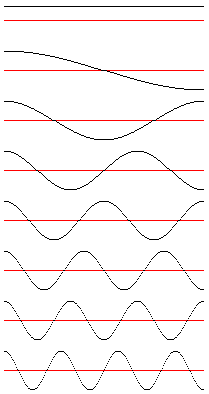
Je représente ici les 8 fonctions de base nécessaire pour décomposer
une rangée de 8 pixels. Pour une rangée de 10 pixels, il en faudrait
10. Si j’en est pris 8 c’est parce que c’est ce que l’on trouve le plus
couramment notamment dans la compression JPEG.
une rangée de 8 pixels. Pour une rangée de 10 pixels, il en faudrait
10. Si j’en est pris 8 c’est parce que c’est ce que l’on trouve le plus
couramment notamment dans la compression JPEG.
Ici, les fonctions sont représentées par beaucoup de point mais lorsque
on les considèrent au moment de faire des calculs, chacune d’entre elle
n’est alors plus que définie par 8 valeurs. C’est valeurs seront représentées
par des colonnes vertes dans les schémas qui suivent.
on les considèrent au moment de faire des calculs, chacune d’entre elle
n’est alors plus que définie par 8 valeurs. C’est valeurs seront représentées
par des colonnes vertes dans les schémas qui suivent.
Le but c’est de trouver la valeur du coefficient qui correspond à chacune de nos fonctions de base. Ce coefficient multiplie la fonction de base. La somme de toute les fonctions de base ainsi redimensionnées doit redonner la forme décrite par la valeur de nos 8 pixels. La valeur de nos 8 pixel est représentée par nos colonnes violettes (une colonne = un pixel). Pour simplifier, on a pris des pixels qui sont en noir et blanc (grande colonne = blanc. colonne null = noir). Le principe pour trouver la valeur de nos coefficients est représenté sur le schéma qui suit.
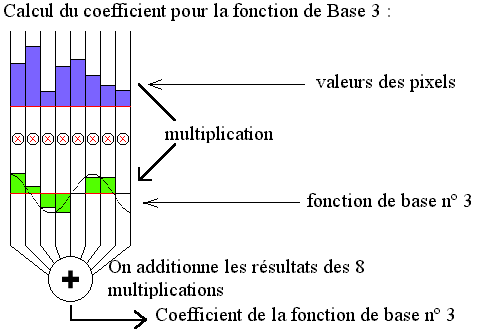
Ici l’exemple est donné pour le calcul de la fonction de base 3, il faut évidemment le faire pour nos 8 fonctions de base. On obtient donc 8 coefficients qui représentent maintenant nos pixels. On a fait notre transformation. C’est maintenant qu’il va y avoir compression (quantization).
Voyons maintenant comment à partir de nos coefficients on peut retrouver
nos pixels d’origine.
nos pixels d’origine.
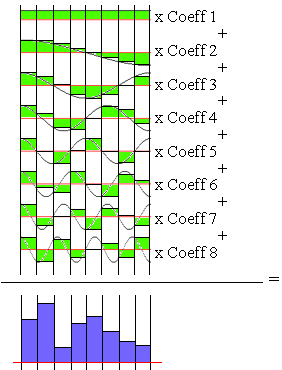Pour reconstituer le pixel 1, on ne s’occupera que de la colonne 1. On prend la valeur de la fonction de base 1 dans la colonne 1 et on la multiplie par le coeff 1. On y additionne la valeur de la fonction de base 2 multiplié par le coeff 2. On additionne à ce résultat la valeur de la fonction de base 3 multiplié par le coeff 3. On fait cela jusqu’à la fonction de base 8 compris et le résultat obtenue donne la valeur d’origine du pixel 1. On fera alors la même chose pour les autres pixels avec leurs colonnes respectives.
La plupart du temps, on décompose des blocs de 8 par 8 pixels sur des fonctions de base en 2D (définit à partir de nos fonctions de base 1D). C’est ce qui est utilisé dans le standard JPEG actuel. L’image est convertie en YUV (luminance chrominance), les valeurs des couches Y, U et V transformées par une DCT 2D en coefficients, les coefficients sont quantifiés (arrondis voir suppression de certain). Ce sont donc ce qu’il reste de coefficient qui est stocké. Enfin, ces coefficients sont compressés avec RLE et Huffman.
Télécharger un programme de démonstration de DCT 1D pour DOS avec le source code en C (23,5 K format zip).
5.1.2 La quantification (arrondir)
C’est dans cette étape qu’il y a vraiment compression. La transformation nous a permit de concentrer l’information importante sur quelques coefficients. On peut donc alors approximer nos coefficients grâce à des « dictionnaires » adaptés. Certains peuvent même être supprimés. Tout ceci réduit donc le nombre de bits qui permettent le stockage de l’image.