1 La base
L’être humain possède deux yeux. Chaque œil lui permet d’avoir une image du monde qu’il observe. Chaque image est une une représentation 2D. C’est grâce à la corrélation de ces deux images que le cerveau développe une représentation 3D du monde observé. La figure qui suit montre comment avec un peu de trigonométrie on peut facilement retrouver l’information de profondeur à partir de deux points de vue. Évidemment, le cerveau ne fait pas de la trigonométrie.
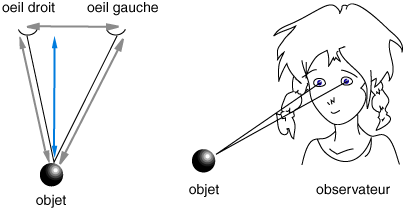
Bon, même si on n’avait pas deux yeux, le cerveau pourrait extrapoler une représentation 3D de notre espace en se servant de nos connaissance et des différents points de vue que l’on peut avoir en déplaçant la tête.
Ce document n’est pas une étude sur le fonctionnement de la perception humaine on ne va donc pas être très rigoureux.
On ne se préoccupera que d’une image et donc que d’un seul œil.
Première approximation, on va considérer l’œil comme un point dans l’espace. Fort de cette hypothèse, regardons ce que l’œil peut observer.
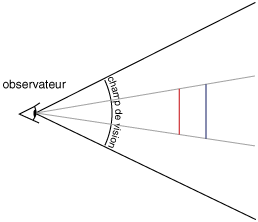
Le champ de vision représente l’angle maximum de ce que l’on peut voir. Dans notre champ de vision, on a placé deux bâtons. Un bleu et un rouge qui est plus proche de l’observateur. Le bâton rouge est plus petit que le bâton bleu. Pourtant, les rayons de lumière qui partent des sommets des bâtons vers l’œil (donc ce que l’œil voit) se superposent. Cela veut dire que les sommets ne forment qu’un seul point sur l’image perçue par l’observateur. En procédant au même raisonnement sur tous les points des deux bâtons on se rend compte que les deux bâtons apparaissent à la même taille sur l’image qu’observe l’œil (bien qu’ici le bâton rouge cache le bâton bleu).
On se rend alors compte que plus les objets sont loin, plus ils apparaissent petit. En effet, dans notre exemple, le bâton bleu apparaît à la même taille que le bâton rouge alors qu’il est plus grand mais il se trouve à une distance plus importante.
Maintenant, si on veut représenter des objets qui n’existent pas, il va falloir simuler leur présence. Pour cela, si on prend un écran, on peut considérer qu’il s’agit d’un plan que l’on place dans le champ de vue de notre oeil.
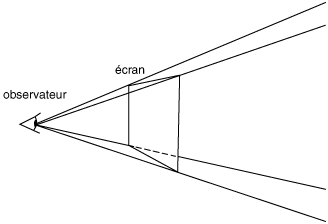
Maintenant, si notre objet n’existe pas on va le représenter sur le plan en 2D de telle sorte que l’objet représenté sur le plan 2D ait la même représentation sur l’œil que l’objet fictif. L’œil ne peut faire la différence puisqu’il s’agit de la même image 2D que s’il observait vraiment notre objet fictif.
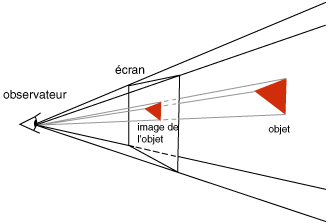
Si on veut que la personne observe la scène en 3D, il faut générer deux images. Une pour chaque œil. La plupart du temps, on en génère qu’une seule et les personnes reconstituent les informations de profondeur en fonction de leurs connaissances et des différentes positions que l’on peut prendre s’il s’agit d’une animation ou si l’observateur a la liberté de se déplacer. Les ombres et les lumières sont aussi une source importante d’informations pour déduire le volume des objets.
2 La définition d’un repère
Avant d’aller plus loin, fixons notre représentation des points dans l’espace. Si on veut donner la position d’un point dans un espace 3D, il nous faut 3 vecteurs non-colinéaires (qui n’évoluent pas dans la même direction). Un point est alors défini par une combinaison de chacun de ces vecteurs. Pour des raisons de simplicité, on prendra un repère (3 vecteurs) orthonormé (chaque vecteur est perpendiculaire au plan formé par les deux autres vecteurs et sa norme est 1).
Voici deux types de repère en fonction de l’orientation du vecteur sur lequel évolu la coordonnée de profondeur :
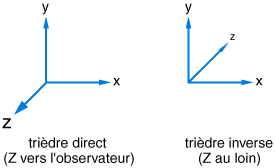
Ce sont les deux repères les plus utilisés, nous prendrons le trièdre direct dans le reste de ce cours.
Tout point dans l’espace est alors représenté par un triplet. On utilise souvent la notation (x,y,z) pour désigner ce triplet. Un point est alors donné par : x*i+y*j+z*k si nos 3 vecteurs sont i (axe des x), j (axe des y) et k (axe des z).
Pour des raisons de simplification, on va considérer que le plan de l’écran correspond au plan i,j et que l’œil est placé sur l’axe des z (colinéairement au vecteur k). L’œil étant à la position (0,0,0) à une distance f du plan écran.
| Code C |
|
Nous définirons un point dans l’espace comme suit :
/* définition d'un point dans un repère 3d */
typedef struct {
float x,y,z;
} dot_3d;
Un objet 3D sera défini comme suit. Un objet est défini avec un ensemble de de point 3D stocké dans le tableau dot de taille nb_dot. C’est points sont utilisés pour définir des faces. Les faces qui forment l’objet sont défini dans le tableau face de taille nb_face. La définition d’une face est présenté un peu plus bas.
/* type de remplissage */
typedef enum{FLAT, GOURAUD, PHONG} FillMode;
/* définition d'un objet 3d */
typedef struct {
/* type de remplissage */
FillMode fill_mode;
/* numéro d'identifiant de l'objet (utilise dans obj_buf) */
uint32 id;
/* nombre de polygone de cet objet */
uint32 nb_face;
/* définition de tout les polygones */
face *face;
/* nombre de point de cet objet */
uint32 nb_dot;
/* définition de tout les points (utilisé dans les polygones) */
dot_3d *dot;
/* tampon pour les calculs des points de l'objet apres transformation */
dot_3d *dot_tmp;
/* vecteur normaux (utilise dans les polygones) par face */
dot_3d *normal;
/* vecteur normaux en chaque sommet de chaque face */
dot_3d *normal_dot;
/* transformation à appliquer sur l'objet (null si aucune) */
float *obj_mat;
/* temporaire, juste pour la démo */
color obj_color;
} obj_3d;
Voici donc la présentation de la définition d’une face. Une face est définie par trois points qui sont réunit pour former la face. Les points sont stockés dans la face comme un index dans le tableau dot de la définition de l’objet auquel appartiennent ces faces. Les index sont pt1, pt2 et pt3.
/* definition d'un polygone */
typedef struct {
/* indice dans le tableau dot des objets */
/* de la définition des trois point du triangle */
/* l'ordre de définition des points doit être */
/* tel que si je ramène le vecteur pt1-pt2 sur */
/* le vecteur pt1-pt3, pt1-pt2 soit sur la main */
/* gauche et pt1-pt3 sur la main droite, et */
/* l'angle pt1-pt2,pt1-pt3 < 180 degrés. Dans */
/* Cette configuration, la normale doit sortir */
/* par la tête. */
uint32 pt1,pt2,pt3;
/* coefficient de réflection diffuse 0.0 <= coef <= 1.0 */
float diffuse;
/* coefficient de réflection spéculaire 0.0 <= coef <= 1.0 */
float speculaire;
/* coeff qui permet de régler la taille des tâches */
/* de la réflexion spéculaire. (par exemple, 1.0 ... 20.0) */
float shine;
} face;
|
3 La projection
La projection est la transformation qui permet de donner la position du point image sur le plan à partir d’un point dans l’espace. Il s’agit donc de déterminer ce que l’on doit dessiner sur le plan de l’écran pour que l’observateur voit la même chose sur le plan que s’il observait vraiment l’objet.
Pour cela, rien de bien compliqué, il suffit de faire intervenir le théorème de Thalès.
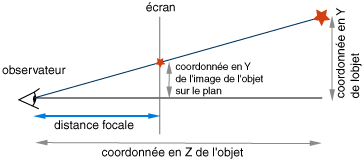
On obtient :
coordonnée en y de l’image de l’objet = (distance focale * coordonnée en y de l’objet) / (-coordonnée en z en l’objet)
On utilise (-coordonnée en z en l’objet) à cause de l’orientation de notre repère.
Ce qui pourrait facilement se traduire en C par :
image_x = (distance_focale * x) / (-z);
image_y = (distance_focale * y) / (-z);
Les points images obtenus sont dans le repère de l’écran si le repère de l’écran est défini comme suit :
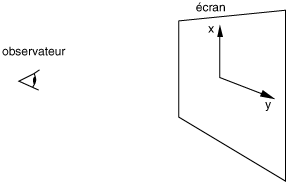
Si ce n’est pas le cas, il faut transformer les coordonnées de l’image pour les faire correspondre au repère de l’écran.
Ce qu’il faut aussi faire c’est tenir compte de la taille des pixels sur l’écran. Mais cela ne change pas le principe.
| Code C |
|
Nous définirons un point 2D sur l’écran comme suit :
/* définition d'un point dans un repère 2d */
typedef struct
float x,y;
dot_2d;
Comme nous l’avons vue, nous avons besoin de la distance focal pour effectuer une projection. De même, si le repère utilisé pour définir le point sur l’écran ne correspond pas au repère de avec le point (0,0) au centre de l’écran, les abscisses étant de définis croissants de gauche à droite et les ordonnées croissantes de bas en haut, nous devons transformer le point pour le définir dans notre repère d’écran. Dans notre cas, nous définissons le coin haut à gauche de l’écran comme le point (0,0). Les abscisses sont définis croissants de gauche à droite et les ordonnées croissantes de haut en bas. La valeur maximum des abscisses et des ordonnées étant définis en fonction de la résolution de l’écran (par exemple (639,479) pour un écran en 640×480).
De même, les pixels ne sont pas forcément carrés. Dans ce cas, il faut tenir compte de ce rapport. Pour tenir compte de tous cela, nous conservons la taille de l’écran ainsi que la distance focale et tous ce que nous avons besoin pour calculer l’image dans une structure qui est définie juste en dessous. Nous avons défini la distance focale sur les abscisses et sur les ordonnées. Cela n’a pas de sens mais en réalité, nous ne conservons pas la distance focale mais le distance focale multiplié par la taille d’un pixel sur les abscisses et sur les ordonnées ce qui nous donne bien 2 valeurs. Voici donc la définition avec beaucoup d’autres champs que nous expliqueront plus tard (pour l’instant on ne s’intéresse qu’à width, height, focal_x et focal_y) :
typedef struct
/* dimension de l'image 3d (utile pour la taille du zbuf et obj_buf) */
int32 width,height;
/* distance de la focal */
float focal_x,focal_y;
/* zbuffer pour décider si un point est caché ou pas */
float *zbuf;
/* indique les objects visibles en chaque point. NULL si non utilise */
uint32 *obj_buf;
/* matrice de transformation à appliquer sur tout les objets (NULL si aucune) */
float *global_mat;
/* liste des objets */
obj_list list;
/* pour la lumière */
float ambiante;
/* liste des lumières utilisées */
List *light_list;
image_3d;
La fonction qui transforme un point 3D en un point 2D sur l’écran s’écrit alors comme suit :
/**************************************************************/
/* projection du point src sur l'écran (coordonnées dans dst) */
void project(image_3d *pimage_3d, dot_2d *dst, dot_3d *src)
if(src->z != 0.0)
dst->x = ((pimage_3d->focal_x * src->x) / (-src->z)) + (pimage_3d->width >> 1);
dst->y = (pimage_3d->height >> 1) - ((pimage_3d->focal_y * src->y) / (-src->z));
else
/* pour éviter une division par 0, on considère que z = 1 */
dst->x = (pimage_3d->focal_x * src->x) + (pimage_3d->width >> 1);
dst->y = (pimage_3d->height >> 1) - (pimage_3d->focal_y * src->y);
/**************************************************************/
Dans cette fonction, un effectue la projection et aussi la transformation des coordonnées résultats pour les exprimer dans notre repère 2D à nous. Pour projeter une face, il suffit de projeter les points des trois sommets de la face pour obtenir trois point sur notre écran. Il suffit de dessiner la face en 2D avec c’est 3 points pour avoir la face 3D projetée.
|
|
4 Les matrices
Pour des raisons de simplicité dans les manipulations, on se sert souvent de la notation des matrices pour modéliser les différentes transformations et notamment les transformations des sommets d’un objet.
Comme on veut pouvoir modéliser toutes les transformations à l’aide des matrices, on utilise des matrices 4×4 et on considère qu’un point est défini par (x,y,z,w) ou w correspond à un facteur d’échelle. On passe de la représentation (x’,y’,z’,w’) à la représentation (x,y,z) en prenant (x’/w’,y’/w’,z’/w’). Dans l’autre sens, il suffit de fixer w à 1.
Voici les matrices pour quelques transformation dans l’espace :
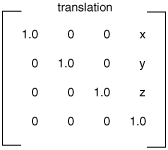


On note alors une transformation comme suit :

| Code C |
|
La première chose à définir est la manière de représenter
une matrice en C. Dans notre convention, une matrice est
un tableau de 16 float, les matrices sont donc de 4 par 4.
Les valeurs sont repartie a des offset comme suit :
| 0 |
1 |
2 |
3 |
| 4 |
5 |
6 |
7 |
| 8 |
9 |
10 |
11 |
| 12 |
13 |
14 |
15 |
|
Maintenant que nous avons la définition d’une matrice en
C, la première chose que nous allons faire c’est voir comment
s’écrit la transformation d’un point par une matrice.
/*********************************************************/
/* transforme le point psrc en pdst avec la matrice pmat */
/* psrc est pdst ne DOIVENT pas pointer sur le m endroit */
/* pdst = pmat * psrc */
void trans_pix(dot_3d *pdst, dot_3d *psrc, float *pmat)
float w;
/* si il n'y a pas de matrice pour la transformation, */
/* on considère qu'il s'agit d'une identitée. */
if(pmat == NULL)
*pdst = *psrc;
return;
/* c'est le produit ligne colonne */
w = pmat[12]*psrc->x + pmat[13]*psrc->y + pmat[14]*psrc->z + pmat[15];
pdst->x = pmat[ 0]*psrc->x + pmat[ 1]*psrc->y + pmat[ 2]*psrc->z + pmat[ 3];
pdst->y = pmat[ 4]*psrc->x + pmat[ 5]*psrc->y + pmat[ 6]*psrc->z + pmat[ 7];
pdst->z = pmat[ 8]*psrc->x + pmat[ 9]*psrc->y + pmat[10]*psrc->z + pmat[11];
/* on supprime le facteur d'échelle */
if(w != 0.0)
pdst->x /= w;
pdst->y /= w;
pdst->z /= w;
/*********************************************************/
Pour pouvoir réaliser une transformation, il faut initialiser
la matrice de transformation en fonction de la transformation
à faire. Pour cela nous allons créer plusieurs fonctions
qui initialiseront les matrices pour les transformations les
plus courantes.
/***************************************************************/
/* génère une matrice de translation dans pmat pour translater */
/* du vecteur (0.0,0.0,0.0) vers vecteur */
void move_mat(dot_3d *vecteur, float *pmat)
pmat[ 0] = 1.0; pmat[ 5] = 1.0; pmat[10] = 1.0; pmat[15] = 1.0;
pmat[ 3] = vecteur->x;
pmat[ 7] = vecteur->y;
pmat[11] = vecteur->z;
/* tout le reste a 0 */
pmat[ 1] = 0.0; pmat[ 2] = 0.0; pmat[ 4] = 0.0; pmat[ 6] = 0.0; pmat[ 8] = 0.0;
pmat[ 9] = 0.0; pmat[12] = 0.0; pmat[13] = 0.0; pmat[14] = 0.0;
/***************************************************************/
/***************************************************************************/
/* génère une matrice de zoom de factor. factor = 1.0 => aucun changement */
void zoom_mat(float factor, float *pmat)
pmat[ 0] = factor; pmat[5] = factor; pmat[10] = factor;
pmat[15] = 1.0;
/* tout le reste a 0 */
pmat[ 1] = 0.0; pmat[ 2] = 0.0; pmat[ 3] = 0.0; pmat[ 4] = 0.0;
pmat[ 6] = 0.0; pmat[ 7] = 0.0; pmat[ 8] = 0.0; pmat[ 9] = 0.0;
pmat[11] = 0.0; pmat[12] = 0.0; pmat[13] = 0.0; pmat[14] = 0.0;
/***************************************************************************/
/*************************************************************/
/* génère une matrice de rotation autour de l'axe x */
/* angle est compris entre 0 (0 degrés) et 1023 (359 degrés) */
void x_rot_mat(int32 angle, float *pmat)
pmat[ 5] = cos_func(angle);
pmat[ 6] = -sin_func(angle);
pmat[ 9] = sin_func(angle);
pmat[10] = cos_func(angle);
pmat[ 0] = 1.0; pmat[15] = 1.0;
/* tout le reste avec des 0 */
pmat[ 1] = 0.0; pmat[ 2] = 0.0; pmat[ 3] = 0.0; pmat[ 4] = 0.0;
pmat[ 7] = 0.0; pmat[ 8] = 0.0; pmat[11] = 0.0; pmat[12] = 0.0;
pmat[13] = 0.0; pmat[14] = 0.0;
/*************************************************************/
/*************************************************************/
/* génère une matrice de rotation autour de l'axe y */
/* angle est compris entre 0 (0 degrés) et 1023 (359 degrés) */
void y_rot_mat(int32 angle, float *pmat)
pmat[ 0] = cos_func(angle);
pmat[ 8] = -sin_func(angle);
pmat[ 2] = sin_func(angle);
pmat[10] = cos_func(angle);
pmat[ 5] = 1.0; pmat[15] = 1.0;
/* tout le reste avec des 0 */
pmat[ 1] = 0.0; pmat[ 3] = 0.0; pmat[ 4] = 0.0; pmat[ 6] = 0.0;
pmat[ 7] = 0.0; pmat[ 9] = 0.0; pmat[11] = 0.0; pmat[12] = 0.0;
pmat[13] = 0.0; pmat[14] = 0.0;
/*************************************************************/
/*************************************************************/
/* génère une matrice de rotation autour de l'axe z */
/* angle est compris entre 0 (0 degrés) et 1023 (359 degrés) */
void z_rot_mat(int32 angle, float *pmat)
pmat[ 0] = cos_func(angle);
pmat[ 1] = -sin_func(angle);
pmat[ 4] = sin_func(angle);
pmat[ 5] = cos_func(angle);
pmat[10] = 1.0; pmat[15] = 1.0;
/* tout le reste avec des 0 */
pmat[ 2] = 0.0; pmat[ 3] = 0.0; pmat[ 6] = 0.0; pmat[ 7] = 0.0;
pmat[ 8] = 0.0; pmat[ 9] = 0.0; pmat[11] = 0.0; pmat[12] = 0.0;
pmat[13] = 0.0; pmat[14] = 0.0;
/*************************************************************/
Un des gros avantages avec les matrices, c’est que l’on peut
facilement combiner les transformations. En effet, si je veut
faire tourner un point puis ensuite le translater, je peux
très bien appliquer la transformation de rotation sur les
coordonnés du point, récupérer les nouvelles coordonnés puis
appliquer sur le résultat la transformation de translation.
Maintenant, je peux aussi créer une transformation qui fait
à la fois la rotation et la translation. Pour cela il faut
multiplier les matrices des deux transformations de base
et utiliser la matrice résultant de la multiplication comme
matrice de transformation. L’opération de multiplication
des matrices (combinaison des transformations) s’écrit comme
suit :
/**************************************************************************/
/* multiplie la matrice p1 par p2, la matrice résultante est pdst */
/* ATTENTION, pdst ne doit pas pointer sur les même matrices que p1 et p2 */
/* pdst = p1 * p2 */
void mul_mat(float *pdst, float *p1, float *p2)
/* première colonne */
pdst[ 0] = (p1[ 0]*p2[ 0])+(p1[ 1]*p2[ 4])+(p1[ 2]*p2[ 8])+(p1[ 3]*p2[12]);
pdst[ 4] = (p1[ 4]*p2[ 0])+(p1[ 5]*p2[ 4])+(p1[ 6]*p2[ 8])+(p1[ 7]*p2[12]);
pdst[ 8] = (p1[ 8]*p2[ 0])+(p1[ 9]*p2[ 4])+(p1[10]*p2[ 8])+(p1[11]*p2[12]);
pdst[12] = (p1[12]*p2[ 0])+(p1[13]*p2[ 4])+(p1[14]*p2[ 8])+(p1[15]*p2[12]);
/* deuxième colonne */
pdst[ 1] = (p1[ 0]*p2[ 1])+(p1[ 1]*p2[ 5])+(p1[ 2]*p2[ 9])+(p1[ 3]*p2[13]);
pdst[ 5] = (p1[ 4]*p2[ 1])+(p1[ 5]*p2[ 5])+(p1[ 6]*p2[ 9])+(p1[ 7]*p2[13]);
pdst[ 9] = (p1[ 8]*p2[ 1])+(p1[ 9]*p2[ 5])+(p1[10]*p2[ 9])+(p1[11]*p2[13]);
pdst[13] = (p1[12]*p2[ 1])+(p1[13]*p2[ 5])+(p1[14]*p2[ 9])+(p1[15]*p2[13]);
/* troisième colonne */
pdst[ 2] = (p1[ 0]*p2[ 2])+(p1[ 1]*p2[ 6])+(p1[ 2]*p2[10])+(p1[ 3]*p2[14]);
pdst[ 6] = (p1[ 4]*p2[ 2])+(p1[ 5]*p2[ 6])+(p1[ 6]*p2[10])+(p1[ 7]*p2[14]);
pdst[10] = (p1[ 8]*p2[ 2])+(p1[ 9]*p2[ 6])+(p1[10]*p2[10])+(p1[11]*p2[14]);
pdst[14] = (p1[12]*p2[ 2])+(p1[13]*p2[ 6])+(p1[14]*p2[10])+(p1[15]*p2[14]);
/* quatrième colonne */
pdst[ 3] = (p1[ 0]*p2[ 3])+(p1[ 1]*p2[ 7])+(p1[ 2]*p2[11])+(p1[ 3]*p2[15]);
pdst[ 7] = (p1[ 4]*p2[ 3])+(p1[ 5]*p2[ 7])+(p1[ 6]*p2[11])+(p1[ 7]*p2[15]);
pdst[11] = (p1[ 8]*p2[ 3])+(p1[ 9]*p2[ 7])+(p1[10]*p2[11])+(p1[11]*p2[15]);
pdst[15] = (p1[12]*p2[ 3])+(p1[13]*p2[ 7])+(p1[14]*p2[11])+(p1[15]*p2[15]);
/**************************************************************************/
La transformation d’une face n’est rien d’autre que la transformation
des sommets de la face.
|
|










